1 砂輪截形的計算
加工汽輪機葉片用葉根銑刀要求精度高、耐磨損且能多次重復使用。該銑刀齒形的軸向截形如圖1所示。圖中A2B及IJ兩段直線垂直于X軸,若采用普通鏟磨法加工刀具齒形,則在該兩段直線處不能形成側后角,刀具用于切削時將首先在此處磨鈍,即產生“勒刀”現象。若采用分段鏟磨方法,即先鏟磨A2B和IJ段之外的曲線,再斜向鏟磨這兩段直線,雖可保證前刃面齒形,但在重磨后齒形將發生改變,影響零件加工精度。若采用整體斜向鏟磨法,則HG 直線段的尺寸難以控制。為解決這一問題,在實際生產中可采用修形砂輪輥子對A~G和H~Z兩段分別進行斜向鏟磨,這種加工方法既可保證刀具重磨后的齒形,又可節省刀具制造工時。

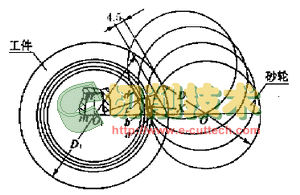
如圖2所示,對銑刀進行徑向鏟磨時,為計算砂輪截形,需已知以下參數:工件截形深度api,被鏟磨銑刀外徑處端面前角gfa,被鏟磨銑刀半徑r0,被鏟磨銑刀齒形上任一點A的極角di,銑刀截形寬度li,被鏟磨銑刀上任一點A處的矢徑ri,被鏟磨銑刀齒數z0,鏟背量K。銑刀軸向截形A點處的坐標為Ti(計算時將各點軸向齒形的縱坐標代入即可),則徑向鏟磨時砂輪截形的計算公式為ri=r0-Ti
di=arcsin[(r0/ri)singfa]-gfa
對于已給定的工件(銑刀),將各段的軸向齒形坐標代入迭代公式,即可計算出q=0°時的砂輪截形GX(I)和GY(I)。

圖2 砂輪截形的計算
2 影響砂輪截形的因素分析
斜向鏟磨時,砂輪既有鏟背運動(阿基米德螺旋運動),又有斜向分運動,此時砂輪截形主要受斜鏟角度q、砂輪直徑D、工件幾何參數等因素的影響。斜鏟角度q的影響
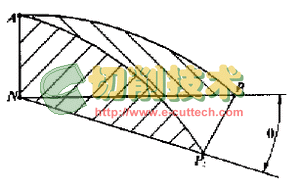
如圖3所示,如采用相同的鏟背量K,因為NP1=K/tana1,NP2=K/tana2(a1,a2分別為A點處的徑向和斜向頂刃后角),又因為NP1=NP2cosq,所以tana2=tana1cosq,即徑向和斜向的頂刃后角不同。如徑向和斜向頂刃后角相同,即a1=a2,則可得K2=K1/cosq,即K值增大。將切削刃上A點的法向后角記為anA,它與鏟磨后角的關系為tananA=tana2sinq。因為tana2=tana1cosq,所以tananA=(1/2)tana1sin2q,即sin2q=2tananA/tana1。
在實際生產中,可根據加工需要選擇斜鏟角度q值,從而確定當量工件直徑D1的值。為保證A2B處良好的切削性能,通常選取anA=3°
砂輪直徑D的影響
如圖4所示,設X為下一個刀齒的頂點,則斜向鏟磨時要求當砂輪直徑上的點尚未到達或剛好到達X點時,凸輪必須回程,否則將會破壞下一個刀齒的軸向截形。根據砂輪結構特點可知,砂輪最小直徑的最大值應為?75mm,由此可推斷出鏟背量K值約為2,將D1及K=2代入迭代公式,并重新計算齒形坐標點,即可得到砂輪的實際截形。
另外,由于對刀不可能十分準確,因此應考慮鏟磨時砂輪串位的需要。為此,應對砂輪輥子相應段的尺寸作相應調整。


 手機資訊
手機資訊 官方微信
官方微信








 豫公網安備41019702003604號
豫公網安備41019702003604號