相對(duì)于傳統(tǒng)砂輪，單層釬焊CBN砂輪在磨削航空航天鈦合金、高溫合金等難加工材料中顯示出低磨削力、高加工效率等優(yōu)勢[1?2]。其根本原因是釬料合金與CBN磨粒、砂輪基體之間實(shí)現(xiàn)了高強(qiáng)度的化學(xué)結(jié)合，提高了砂輪基體對(duì)CBN磨粒的把持力[3]。目前，常見的釬焊方法主要包括真空爐中釬焊[4]、感應(yīng)釬焊[5]以及激光釬焊[6]三種。其中，感應(yīng)釬焊工藝具有釬焊周期短、低成本、可局部加熱等特點(diǎn)，在單層釬焊CBN砂輪領(lǐng)域獲得了廣泛的應(yīng)用和研究。研究表明，提高感應(yīng)電流的頻率，可以實(shí)現(xiàn)CBN砂輪的局部釬焊，從而有效減少釬焊熱影響區(qū)，提高釬焊砂輪的精度[7]。然而，成型砂輪的感應(yīng)釬焊一直是研究中的難點(diǎn)，其原因在于感應(yīng)加熱過程中的集膚效應(yīng)和邊緣效應(yīng)[8]極容易引起橫截面輪廓曲線復(fù)雜的成型砂輪表面溫度分布不均勻，從而導(dǎo)致無法滿足砂輪釬焊質(zhì)量一致性的要求。

       感應(yīng)加熱溫度場的影響因素較多且規(guī)律復(fù)雜，國內(nèi)外的相關(guān)研究以有限元數(shù)值仿真為主。例如Barka等[9]采用有限元法研究了齒輪表面感應(yīng)淬火的溫度場，發(fā)現(xiàn)電流強(qiáng)度和頻率對(duì)齒根和齒頂?shù)臏囟确植加兄匾挠绊憽８邜鸬萚10]就平面的單回線感應(yīng)加熱問題進(jìn)行了仿真研究，指出導(dǎo)磁體磁軛尺寸、電流頻率以及電流強(qiáng)度等參數(shù)在合理的范圍內(nèi)能獲得最佳加熱效率和溫度均勻性。童欣等[11]針對(duì)單層釬焊超硬磨料成型砂輪感應(yīng)加熱時(shí)存在的溫度分布不均勻問題，借助有限元仿真軟件在研究線圈與導(dǎo)磁體的結(jié)構(gòu)尺寸對(duì)溫度分布的影響規(guī)律的基礎(chǔ)上，設(shè)計(jì)了感應(yīng)器用于成型砂輪的釬焊。以上研究結(jié)果表明，感應(yīng)電流和感應(yīng)器結(jié)構(gòu)是影響溫度場的重要因素，但由于感應(yīng)加熱過程中材料物理屬性的非線性特征，導(dǎo)致難以獲得最佳工藝參數(shù)以及最優(yōu)的感應(yīng)器結(jié)構(gòu)。

       響應(yīng)曲面法（response surface methodology，RSM）結(jié)合了數(shù)學(xué)方法和統(tǒng)計(jì)方法，專門用來研究響應(yīng)值受多個(gè)變量影響進(jìn)行建模與分析，最終優(yōu)化該響應(yīng)值[12?13]。該方法最早由Box和Wilson于1951年提出，隨后在優(yōu)化設(shè)計(jì)、可靠性分析等領(lǐng)域獲得廣泛應(yīng)用。成型面感應(yīng)加熱溫度場的控制屬于典型多目標(biāo)優(yōu)化問題，目前RSM在感應(yīng)加熱領(lǐng)域已有不少研究報(bào)道。例如清華大學(xué)李峰等[14]針對(duì)平面單回線感應(yīng)加熱過程中的能量傳遞機(jī)理進(jìn)行了研究，通過響應(yīng)曲面法分析了影響溫度精確性的工藝參數(shù)。Khalifa等[15]采用響應(yīng)曲面法與人工神經(jīng)網(wǎng)絡(luò)結(jié)合的方法研究了齒輪表面感應(yīng)淬火溫度場的影響因素，最終準(zhǔn)確預(yù)測了齒輪表面溫度分布與淬火深度。這些研究結(jié)果表明RSM在感應(yīng)加熱過程中工藝參數(shù)優(yōu)化等方面具有明顯的優(yōu)勢。

       本文基于RSM分析成型砂輪感應(yīng)釬焊的溫度分布的影響因素，以溫度均勻度和平均溫度為目標(biāo)，建立2階預(yù)測模型描述目標(biāo)響應(yīng)值與設(shè)計(jì)變量之間的關(guān)系，為研制高性能的單層釬焊成型砂輪奠定理論基礎(chǔ)。

       1 研究對(duì)象與方案設(shè)計(jì)

       1.1 有限元模型

       圖1所示為用于鈦合金葉片榫齒成型磨削的燕尾槽成型砂輪基體尺寸示意圖，其材料為45鋼。可以看出該砂輪工作面輪廓的曲率半徑較小，分別為1.5 mm和1.6 mm，圖中R為半徑，為直徑。

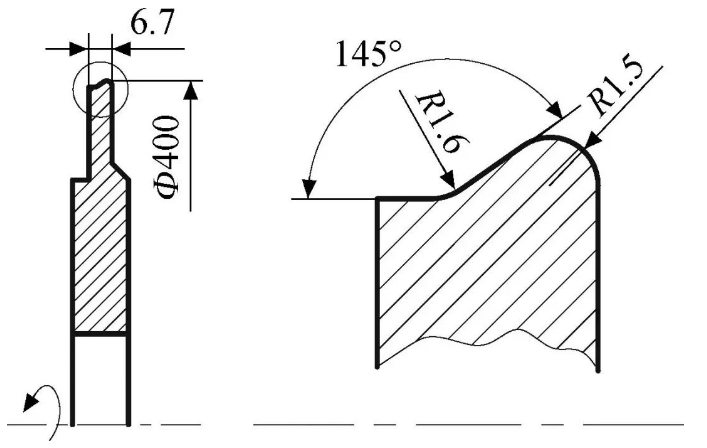
圖1   燕尾槽成型砂輪基體尺寸示意圖（單位：mm）

Fig.1   Geometry scheme of dovetail slot profiled grinding wheel matrix （unit：mm）

       幾何模型如圖2（a）所示。考慮到模型的對(duì)稱性，幾何模型只有1/2。模型包括砂輪基體、紫銅管線圈、導(dǎo)磁體以及空氣。需要指出的是，建模時(shí)將圓形砂輪基體簡化為直工件，其高度為273 mm，用于等效砂輪的徑向厚度。線圈橫截面尺寸為2 mm×2.5 mm（實(shí)際加熱過程中，紫銅管線圈中間有直徑1 mm的孔，孔內(nèi)部通入增壓的冷卻水），采用仿形結(jié)構(gòu)，加熱間隙（即與工件之間的距離）為h。導(dǎo)磁體為Ferritron 559H羰基鐵，材料屬性參見文獻(xiàn)[16]，其長度為L。

圖2   有限元模型示意圖

Fig.2   Scheme of finite element model

       根據(jù)有限元計(jì)算原理，在線圈和工件的集膚深度內(nèi)必須有至少2層網(wǎng)格才能保證計(jì)算精度，而這樣會(huì)導(dǎo)致網(wǎng)格量巨大，影響效率。因此本文中，工件設(shè)置了表面阻抗邊界條件[17]來避免較細(xì)的網(wǎng)格。另外，采用非網(wǎng)格化線圈來等效實(shí)際的線圈。在有限元計(jì)算時(shí)，該線圈不需要?jiǎng)澐志W(wǎng)格，僅需加載電流，電磁耦合采用Biot?Savart公式計(jì)算，收斂性較好[18]。上述簡化處理能夠在保證計(jì)算精度的前提下極大提高計(jì)算效率。最終網(wǎng)格總數(shù)約為5.8萬，如圖2（b）所示。

       1.2 釬焊溫度表征方法

       溫度均勻性對(duì)釬焊接頭質(zhì)量的一致性具有重要影響。為了合理地表征砂輪表面溫度的均勻性，沿砂輪基體輪廓方向等間隔獲取溫度值，可得到溫度序列Ti（i=1,2,…,n），如圖3所示。本文中，沿砂輪基體輪廓線從點(diǎn)a到點(diǎn)b，間隔寬度為0.5 mm，共獲得溫度序列數(shù)n為55個(gè)。

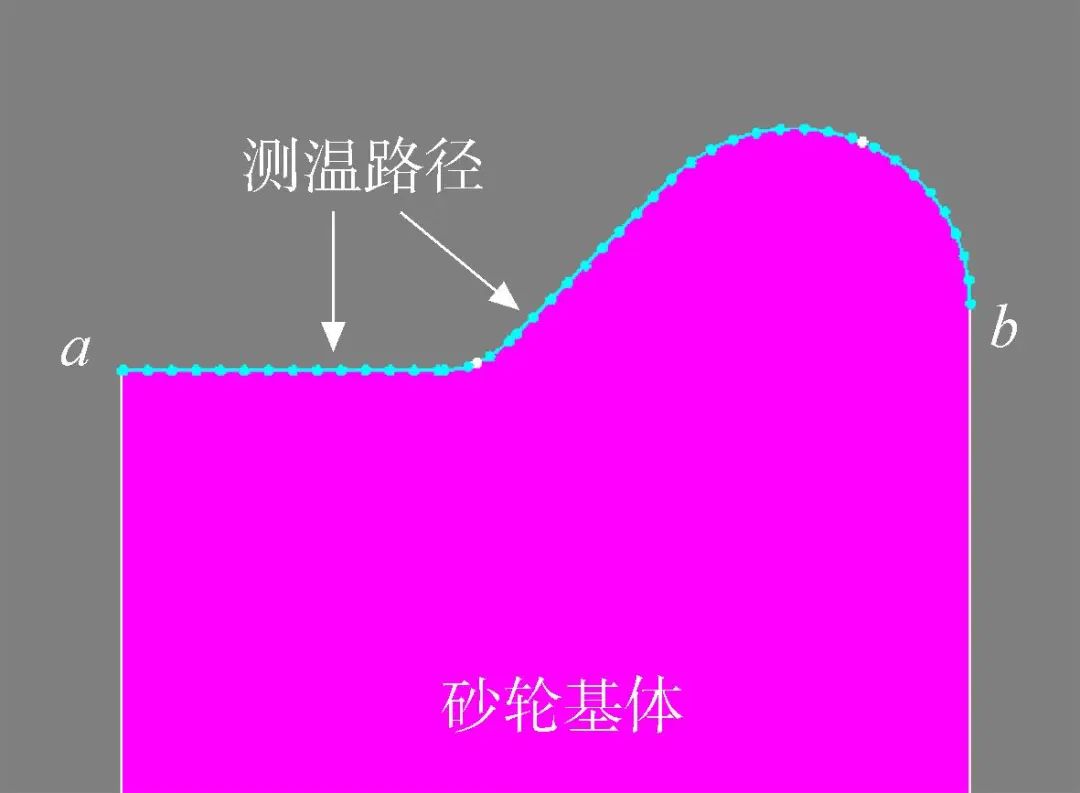
圖3   成型面溫度分析路徑

Fig.3   Measured path for profiled surface temperature analysis

       根據(jù)溫度序列，可得到其均方差為

       式中為平均溫度，是溫度序列的平均值。砂輪基體輪廓溫度均勻度按下式定義：

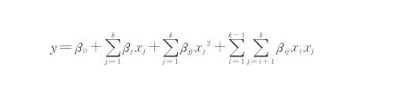
       上述平均溫度和溫度均勻度U兩個(gè)變量共同表征砂輪基體輪廓方向的溫度均勻性。從式（2）可以看出，溫度均勻度U等于100%時(shí)，意味著溫度序列值都相等，即輪廓面上無溫度差異。

       1.3 Box?Behnken試驗(yàn)設(shè)計(jì)

       選擇感應(yīng)電流I，導(dǎo)磁體長度L，加熱間隙h作為設(shè)計(jì)變量，以平均溫度和溫度均勻度U為響應(yīng)值，采用Design?Expert軟件設(shè)計(jì)三因素三水平的仿真方案如表1所示，加熱時(shí)間均為10 s。根據(jù)仿真結(jié)果，采用RSM建立的預(yù)測模型表達(dá)式為[15]

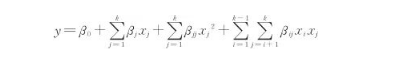
       式中y為響應(yīng)值；xj為第j個(gè)設(shè)計(jì)變量；k為設(shè)計(jì)變量的個(gè)數(shù)，本文中的設(shè)計(jì)變量為3個(gè)，即k=3；β0為常數(shù)，βj為第j線性系數(shù)，βjj為2階偏移系數(shù)，βij為變量交互作用系數(shù)。

表1   響應(yīng)曲面法各因素與水平

Table 1   Factor and level values of RSM

       2 結(jié)果與討論

       2.1 溫度均勻性的響應(yīng)曲面分析

       根據(jù)Box?Behnken方法設(shè)計(jì)的仿真結(jié)果如表2所示。從表中可以看出平均溫度、溫度均勻度兩個(gè)變量與各設(shè)計(jì)因素之間不是線性關(guān)系。根據(jù)RSM，剔除非顯著項(xiàng)，可分別獲得平均溫度和溫度均勻度U兩個(gè)響應(yīng)值的預(yù)測模型為

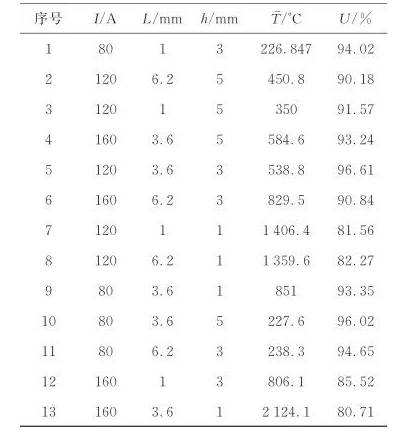
表2   各因素設(shè)計(jì)方案與仿真結(jié)果

Table 2   Design and simulation results of each factors

       為了檢驗(yàn)上述模型是否有效，對(duì)各系數(shù)進(jìn)行方差分析（analysis of variance,ANOVA），結(jié)果分別如表3和表4所示。可以看到兩個(gè)表中：決定系數(shù)R2均接近于1，說明擬合程度較好，且與調(diào)整決定系數(shù)Radj2接近，意味著建立的模型對(duì)擬合的數(shù)據(jù)做出了良好的調(diào)整；兩個(gè)模型的P值（顯著性檢驗(yàn)）均小于0.000 1，表明模型極具有顯著性[14]；另外，根據(jù)表中F值（方差檢驗(yàn)）可以得到各因素對(duì)響應(yīng)值的影響大小，可以看出，三個(gè)因素對(duì)平均溫度和溫度均勻度U的影響的顯著程度由大到小，依次為加熱間隙h、感應(yīng)電流I、導(dǎo)磁體長度L。式（4）中導(dǎo)磁體長度L僅在一次項(xiàng)中出現(xiàn)，且表3所示的方差分析表明該項(xiàng)的P值為0.626 5，P>0.05意味著該項(xiàng)的顯著性比較低，因此RSM模型表明導(dǎo)磁體長度對(duì)平均溫度的影響不顯著。

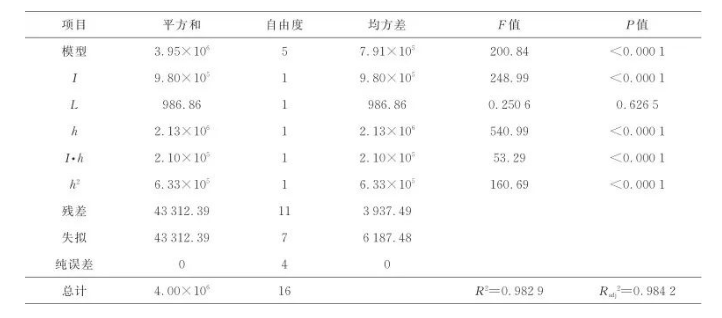
表3   平均溫度的ANOVA結(jié)果

Table 3   ANOVA results of average temperature

表4   溫度均勻度的ANOVA結(jié)果

Table 4   ANOVA results of temperature uniformity

       RSM不僅能夠減少試驗(yàn)次數(shù)，還可以綜合分析各因素交互作用下對(duì)響應(yīng)值的影響。式（3）中的最后一項(xiàng)即表示因素間的交互作用[13]。從響應(yīng)曲面模型式（4）、式（5）可知，平均溫度的影響因素中，僅感應(yīng)電流I和加熱間隙h之間存在交互作用；而溫度均勻度的影響因素中，存在兩項(xiàng)交互作用，即感應(yīng)電流I和導(dǎo)磁體長度L，感應(yīng)電流I和加熱間隙h。其他交互因素由于在響應(yīng)曲面模型擬合過程中不顯著，而被忽略剔除。

       根據(jù)式（4），可以得到感應(yīng)電流I和加熱間隙h交互作用下，對(duì)平均溫度的響應(yīng)曲面如圖4所示。從圖中可以看出，隨著感應(yīng)電流的增加和加熱間隙的減小，平均溫度出現(xiàn)明顯增大。另外，響應(yīng)曲面在加熱間隙坐標(biāo)軸的方向斜率更大，說明相對(duì)于感應(yīng)電流，加熱間隙對(duì)平均溫度的影響更加顯著。響應(yīng)曲面在底面的投影形成的等高線圖的形狀可反映因素間的交互作用，即橢圓形的等高線代表因素間的交互作用明顯，而直線則表示因素間的交互作用不明顯。圖4可以看出感應(yīng)電流與加熱間隙整體的交互作用較少，僅在平均溫度較低的時(shí)候存在一定的交互作用。

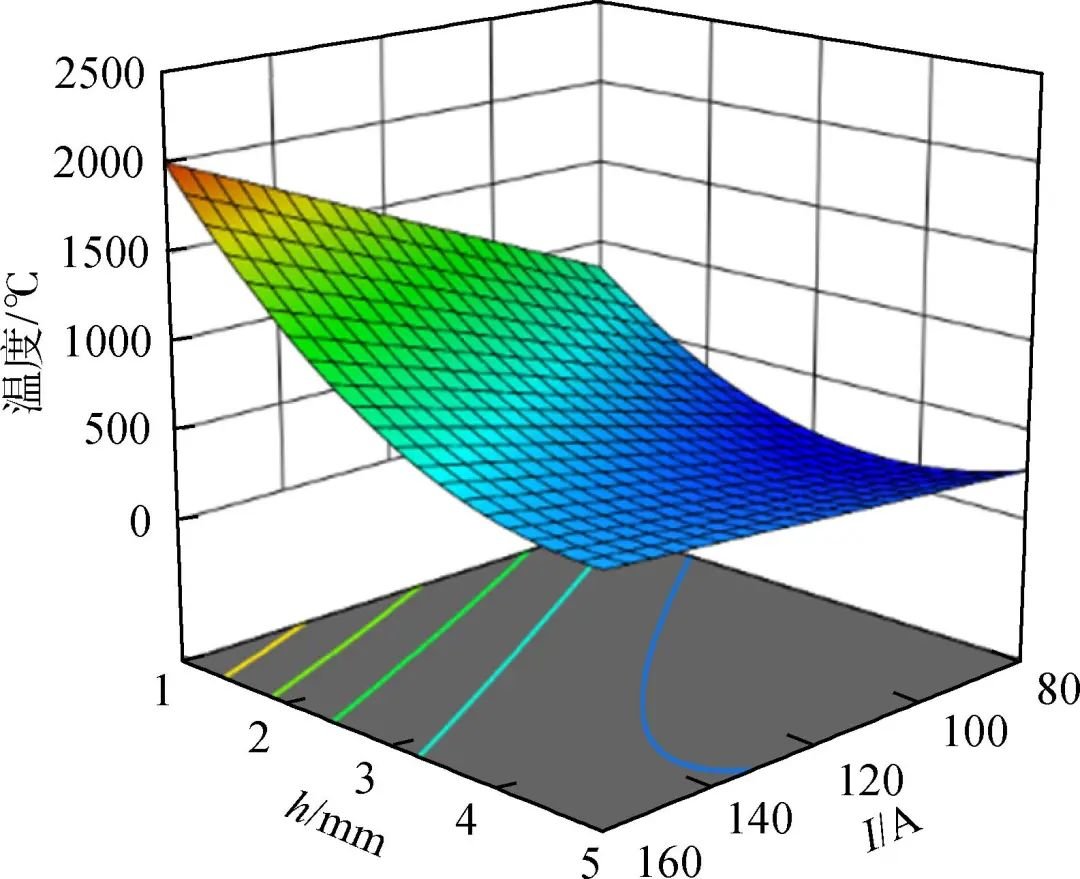
圖4   感應(yīng)電流和加熱間隙對(duì)平均溫度的交互作用

Fig.4   Interaction effect of induction current and heating gap on average temperature

       各因素交互作用下對(duì)溫度均勻度的響應(yīng)曲面如圖5所示。可以看出相對(duì)于平均溫度，溫度均勻度的非線性特征更加明顯。隨著感應(yīng)電流的增加，溫度均勻度呈下降趨勢，而導(dǎo)磁體長度和加熱間隙的增大，會(huì)導(dǎo)致溫度均勻度先上升然后下降。從等高線圖可以看出，感應(yīng)電流與導(dǎo)磁體長度之間的交互作用最為顯著，感應(yīng)電流與加熱間隙之間的交互作用次之。

圖5   各因素對(duì)溫度均勻度的交互作用

Fig.5   Interaction effect of factors on temperature uniformity

       大量研究結(jié)果顯示，導(dǎo)磁體作為一種磁場強(qiáng)化手段，可有效約束局部的磁力線分布，從而提高感應(yīng)加熱的效率[9,19]。本文中，仿形線圈在成型面凸出區(qū)域的加熱效率高，而在內(nèi)凹區(qū)域的加熱效率低，從而導(dǎo)致型面輪廓方向溫差較大。仿真中導(dǎo)磁體長度的最大值為6.2 mm，僅作用在成型面內(nèi)凹的局部區(qū)域，因此其主要作用是提高成型面內(nèi)凹區(qū)域的加熱效率，從而減少整個(gè)型面的溫差。圖6所示為導(dǎo)磁體對(duì)成型砂輪表面溫度場的影響。從圖中可以看出無導(dǎo)磁體時(shí)，型面內(nèi)凹處和凸出部分的溫差比較大，分別為682.9 ℃和916.7 ℃。有導(dǎo)磁體之后，型面溫差明顯減小，其中內(nèi)凹處的溫度提高到791.2 ℃，而凸出部分的溫度變化不明顯，為922.5 ℃。可見，本文條件下導(dǎo)磁體對(duì)平均溫度的影響不明顯，而對(duì)溫度均勻度的影響十分顯著。

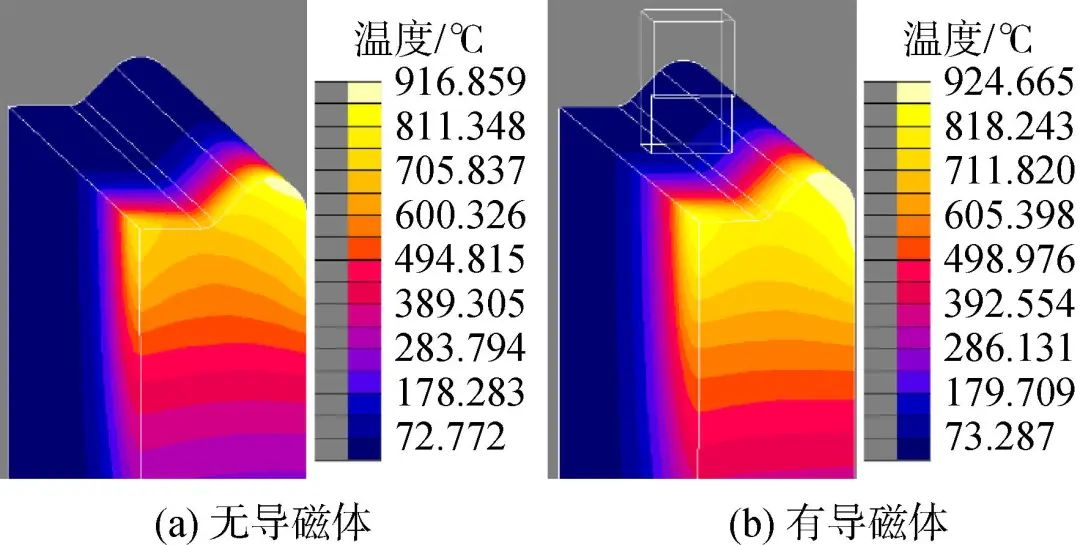
圖6   導(dǎo)磁體對(duì)溫度場的影響

Fig.6   Effect of magnetizer on temperature field

       2.2 感應(yīng)線圈優(yōu)化與試驗(yàn)驗(yàn)證

       前期研究表明Ag?Cu?Ti釬料感應(yīng)釬焊CBN砂輪的最佳釬焊溫度為940 ℃[5]，因此，感應(yīng)線圈的優(yōu)化目標(biāo)是平均溫度為940 ℃，溫度均勻度U為最大化。三個(gè)因素中，加熱間隙對(duì)溫度均勻性的影響最為顯著。另一方面，考慮到加熱間隙太小會(huì)導(dǎo)致在實(shí)際釬焊過程中線圈與CBN磨粒接觸，因此增加了一個(gè)約束條件即加熱間隙h=2 mm。基于相應(yīng)曲面模型，可獲得最優(yōu)參數(shù)為I=124.4 A，L=3.8 mm。此時(shí)預(yù)測模型得到的平均溫度=940 ℃，溫度均勻度U=91.96%。為了驗(yàn)證該最優(yōu)化方案的效果，搭建了如圖7（a）所示的試驗(yàn)裝置。圖中感應(yīng)線圈導(dǎo)磁體長度為3.8 mm，加熱間隙為2 mm，感應(yīng)電流為124.4 A。采用德國OPTRIS PI230型紅外熱像儀進(jìn)行實(shí)時(shí)測溫，其發(fā)射率設(shè)置為0.8。圖7（b）所示為加熱時(shí)間為10 s時(shí)刻工件輪廓表面的溫度分布測量值與仿真結(jié)果對(duì)比。可以看出，仿真結(jié)果顯示工件輪廓測量路徑上的溫度范圍為906.8~1 029.8 ℃，平均溫度為959.6 ℃，溫度均勻度為95.41%.而試驗(yàn)獲得的溫度范圍整體偏低，為903.8~952.7 ℃，平均溫度為924.1 ℃，而溫度均勻度達(dá)到了98.34%，與響應(yīng)曲面預(yù)測模型的誤差分別為1.69%和6.94%。從圖中還可以看出，溫度的試驗(yàn)測量值與仿真結(jié)果之間的誤差最大值為8.75%。造成上述誤差的主要原因可能是有限元模型采用了一定的簡化處理，如工件的表面阻抗邊界條件以及非網(wǎng)格化線圈等，從而導(dǎo)致了仿真結(jié)果的誤差。盡管如此，上述結(jié)果仍然可以證明仿真模型具有一定的準(zhǔn)確性和可靠性。

圖7   感應(yīng)釬焊溫度均勻性優(yōu)化結(jié)果的驗(yàn)證

Fig.7   Veryfication of optimal results of temperature uniformity in induction brazing

       此外，從圖7（b）還可以看出，試驗(yàn)條件下，工件凸出部位的溫度分布明顯低于仿真結(jié)果，誤差相對(duì)較大。可能的原因是試驗(yàn)條件下，受實(shí)際工藝的限制，線圈與工件之間的相對(duì)位置存在一定的偏差，導(dǎo)致實(shí)際的加熱間隙比設(shè)定值稍大。而從溫度均勻性的相應(yīng)曲面分析結(jié)果可知，加熱間隙h對(duì)砂輪表面的溫度影響最為顯著，導(dǎo)致工件表面的實(shí)際加熱溫度比仿真結(jié)果更低。

       2.3 高頻感應(yīng)釬焊成型CBN砂輪試驗(yàn)

       待釬焊的成型砂輪采用無鍍膜CBN磨粒，平均直徑為150~180 μm。釬料為Ag?Cu?Ti合金粉末，主要組分為96（72Ag?28Cu）?4Ti（質(zhì)量分?jǐn)?shù)，%），熔點(diǎn)為880 ℃。高頻感應(yīng)釬焊參數(shù)基于優(yōu)化結(jié)果，即與文中第2.2節(jié)的試驗(yàn)參數(shù)相同。砂輪釬焊原理與釬焊裝置如圖8（a）所示。釬焊時(shí)，采用開放式的局部Ar氣保護(hù)，Ar氣體積流量為40 L/min。

圖8   高頻感應(yīng)釬焊成型CBN砂輪

Fig.8   High frequency induction brazing of profiled CBN grinding wheel

       釬焊CBN砂輪形貌照片如圖8（b）所示。可以看出釬料在成型面各處的鋪展性比較均勻，表明釬焊過程中在成型面的溫度分布具有較好的均勻性。

       3 結(jié) 論

       1） 提出了基于平均溫度和溫度均勻度的成型砂輪感應(yīng)釬焊溫度均勻性表征模型，并采用有限元仿真分析結(jié)果獲得了成型面平均溫度和溫度均勻度的2階響應(yīng)曲面預(yù)測模型，模型擬合程度良好，可用于平均溫度和溫度均勻度的預(yù)測。

       2） 基于預(yù)測模型和方差分析，各因素對(duì)平均溫度和溫度均勻度影響的顯著程度從大到小依次為加熱間隙h、感應(yīng)電流I、導(dǎo)磁體長度L。

       3） 基于響應(yīng)曲面法優(yōu)化線圈結(jié)構(gòu)和工藝參數(shù)，開展了感應(yīng)加熱試驗(yàn)，結(jié)果顯示成型面平均溫度為924.1 ℃，溫度均勻度為98.34%，與響應(yīng)曲面預(yù)測模型的誤差分別為1.69%和6.94%。

       4） 高頻感應(yīng)釬焊成型CBN砂輪宏觀形貌顯示，釬料在成型面各處鋪展的一致性好，表明釬焊過程中在成型面的溫度分布具有較好的均勻性。

       作者簡介：李奇林（1984-），男，副教授、碩士生導(dǎo)師，博士，主要從事超硬磨料砂輪釬焊技術(shù)研究。

       通訊作者：王西超（1982-），男，講師、碩士生導(dǎo)師，博士，主要從事人工智能與數(shù)學(xué)建模研究。E?mail：wangxc@sdju.edu.cn

       基金信息： 國家自然科學(xué)基金（51905234，51805231）

       中圖分類號(hào)： V263.1； TG454

       文章編號(hào)：1000-8055（2022）09-1915-08

       文獻(xiàn)標(biāo)識(shí)碼： A

       收稿日期：2022-01-23

       出版日期：2022-09-28

       網(wǎng)刊發(fā)布日期：2022-10-08

       本文編輯：秦理曼