作者：黃云1,2，桂林1，秦濤3，王文璽1,2，鄒萊1,2，李恒1?

       作者單位：1. 重慶大學 機械與運載工程學院，重慶 400044；2. 高端裝備機械傳動全國重點實驗室，重慶 400044；3. 中國航發南京輕型航空動力有限公司，江蘇 南京 211100

       收稿日期：2023-11-01

       基金項目：重慶市自然科學基金創新群體項目（CSTC2019JCYJ-CXTTX0003），Innovation Group Science Fund of Chongqing Natural Sci?ence Foundation（CSTC2019JCYJ-CXTTX0003）；中央高校基本科研業務費專項資金資助項目（2023CDJXY-022），Fundamental Research Funds for the Central Universities（2023CDJXY-022）；重慶市研究生科研創新項目（CYB23021），Chongqing Graduate Research Innovation Project （CYB23021）

       作者簡介：黃云（1962―），男，重慶萬州人，重慶大學教授，博士生導師

       通信聯系人，E-mail：Heng.Li@cqu.edu.cn

       摘要

       本文提出了一種面向葉片前緣廓形精準控制的機器人砂帶磨削加工方法. 以軸流壓氣機葉片為研究對象，結合半赫茲接觸理論和有限元仿真獲取了柔性磨具和葉片前緣的接觸區域內的應力分布，基于Preston方程求解材料去除函數. 遍歷刀位點對控制點的磨削深度，建立全局材料去除矩陣，搭建駐留時間求解非線性方程組. 采用帶有阻尼因子的Tikhonov正則化消除大型稀疏病態矩陣對求解精度波動的影響，將所求駐留時間轉換為對應刀位點的進給速度，生成機器人加工代碼. 磨削試驗結果表明，基于駐留時間控制的機器人砂帶磨削方法能夠實現給定允差范圍內葉片前緣廓形的精準加工，型面誤差可以控制在0.02 mm以內.

       關鍵詞：壓氣機；砂帶；柔性磨削；前緣廓形；駐留時間

       引言

       航空發動機是飛機的核心部件之一，直接關系到飛機的性能和安全，不僅是國家重點發展領域之一，也是推動國家經濟、科技和軍事發展的重要引擎之一［1］. 葉片前緣的加工直接決定了葉片的氣動性能和服役壽命，然而葉片前緣部分由于曲率變化劇烈、剛性差且彎曲和扭曲程度大，并且使用的鈦合金材料導熱系數低、彈性模量小，屬于典型的難加工部位， 對實現葉片的精密磨削帶來了極大的挑戰［2-5］.

       砂帶磨削是一種柔性加工方法，兼具磨削和拋光功能 . 它具有高效切割、冷態磨削、靈活工藝性和廣泛適應性等諸多優點 . 因此砂帶磨削被廣泛用于精密磨削加工復雜自由曲面，尤其在葉片加工中發揮著重要作用. 它是提高葉片型面精度、表面完整性和加工一致性的有效方法之一 . 面對余量分布不均的葉片加工，需要精確的材料去除函數來開展工藝參與規劃，眾多學者對此做出了大量的研究 . Guo等［6］針對葉片前尾緣的多余材料去除問題提出通過構建臨時引導模型來指導加工過程 . Wan 等［7］利用公差帶來提高葉片定位能力以避免葉片出現過磨 .Wang 等［8］采用非接觸式冷加工方法，針對葉片前緣難加工問題進行了電解加工葉片邊緣的嘗試，通過陰極的刀具沿葉片平均弧度線切向進給，對葉片前、后緣進行電化學加工 . Mu等［9］在葉片加工穩定性方面進行研究，通過機器人七軸聯動砂帶磨削系統的區域力控來實現加工過程中接觸力的實時控制并減少每個區域的力信號波動 . Sarma 等［10］針對數控磨削加工道路軌跡生成進行了研究，提出了一種綜合考慮制造與測量的軌跡生成方法.

       當前學者針對壓氣機葉片邊緣的精準去除已經開展了全面而深入的研究，揭示了加工工藝參數與材料去除之間的緊密聯系 . 但是由于過去的研究都是逐點調控，無法解決砂帶柔性磨削接觸面積大、刀位點之間干涉嚴重的現象，而計算機控制光學表面形成中常用的駐留時間控制加工方法，作為一種全局求解的方法能很好地解決這類問題. 因此，本文根據 Abaqus仿真分析獲得接觸區域的應力分布，代入半赫茲接觸中并對結果進行修正，通過 Preston 方程建立對應區域的去除函數模型；基于全局求解的思想，在葉片表面引入控制點和駐留點，通過遍歷駐留點和控制點的方式獲取砂帶柔性磨削的加工軌跡，考慮了加工時對相鄰刀位點的影響，更符合砂帶柔性磨削加工的特點.

       1葉片前緣去除函數建模

       1.1 Abaqus接觸狀態有限元仿真

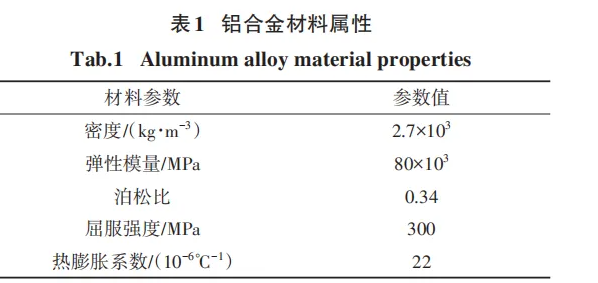
       利用有限元仿真軟件 Abaqus 對葉片前緣和柔性磨具進行接觸狀態的仿真研究 . 首先將葉片的三維模型導入 Abaqus，葉片模型材料為鋁合金，采用Johnson-Cook（JC）本構損傷模型［11］模擬加工葉片時材料的失效狀態. 鋁合金材料屬性如表1所示.

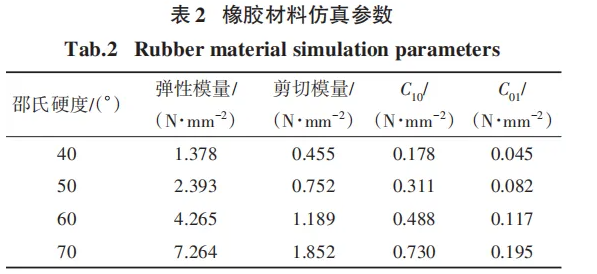
       考慮到有效接觸區域以及減小仿真試驗的計算壓力，接觸輪模型只取了 5% 區域，柔性磨具的材料采用制備接觸輪的丁腈橡膠 . 橡膠材料仿真參數如表 2所示，橡膠材料屬于超彈性材料，且本次仿真試驗屬于小變形的加工范圍，故采用橡膠材料常用的Mooney-Rivlin應力-應變本構模型［12］表示.     

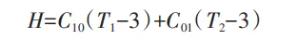
       式中：H為超彈性材料橡膠的應變能密度；T1、T2表示變形張量不變量；C10、C01表示橡膠材料硬度有關的材料彈性系數.

       根據實際加工需求，對葉片施加了榫頭部分的單端固定約束，接觸輪沿葉片邊緣施加垂直于葉片的法向力，網格采用的是以六面體為主的C3D8過渡網格，中間加密處的網格單元尺寸為 0.2，通過觀察接觸部分的應力變化并對其進行分析，該模型能夠準確反映材料在高應變速率下的變形行為，進而為后續研究中建立材料去除模型提供接觸區域的應力分布.

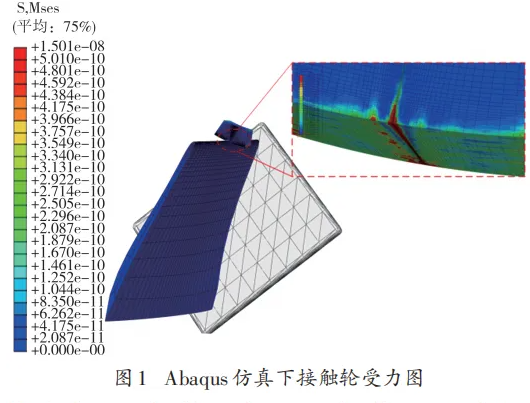
       由于砂帶相對于接觸輪厚度很薄并且產生的變形不明顯，在分析接觸部分的應力變化中影響很小，因此在 Abaqus 中做了簡化處理 . 當下壓量為 3 mm時，Abaqus仿真下接觸輪受力圖如圖1所示，接觸輪與前緣接觸后發生了非線性彈性變形，在接觸區域形成應力集中，接觸區域兩側的應力隨著距離接觸中心增大而減小 . 接觸輪不同截面的應力分布曲線如圖2所示，等效應力狀態云圖近似于正態分布.

       1.2 建立葉片前緣材料去除模型

       Preston方程是被廣泛應用并被證實具有很高可信度的經驗公式. 此方程是由Preston［13］在1927年提出的，即

       式中：dz/dt表示刀位點單位時間內的去除量；k 為比例系數，由除了接觸壓力p和瞬時相對速度v以外的影響因素共同決定，如磨料類型、工件材料等 . 根據Preston方程可以推導出在加工點（x，y）處停留時間T對應的材料去除量：

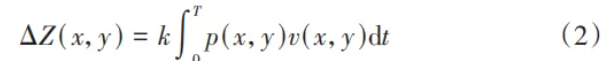
       根據式（2）可推出對應葉片邊緣上任一點的去除函數為：

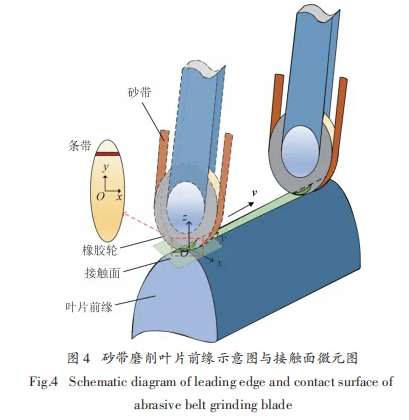
       式中：H（x，y）表示在設定刀位點處的材料去除率.在實際葉片前緣加工過程中，在多種不同的接觸狀態 接觸輪與工件存，如圖 3和圖4 所示 . 圖 3 中R0為接觸輪半徑，l0為橡膠輪寬度，d0為接觸區域的彈性變形高度，Fn表示加工葉片的軸向力，Ft表示工件受到的接觸反力. 根據赫茲接觸理論［14］，當兩個物體接觸并壓緊時，初始接觸點附近的材料會發生局部變形. 彈性接觸理論基于以下假設：①接觸物體只產生彈性變形，并符合胡克定律；②接觸力垂直于接觸面；③接觸面的尺寸遠小于接觸物體表面.

       在接觸輪與葉片的接觸中，邊緣處的材料去除量較小，接觸輪始終保持彈性接觸狀態. 在砂帶磨削過程中，當砂帶繞回轉中心O點勻速轉動時，可以將砂帶和接觸輪視為一個完整的整體，接觸輪與前緣之間存在方向接觸力，前兩個條件符合赫茲接觸理論，由于葉片前緣部分曲率變化大，本文采用半赫茲接觸理論求解接觸應力分布模型.

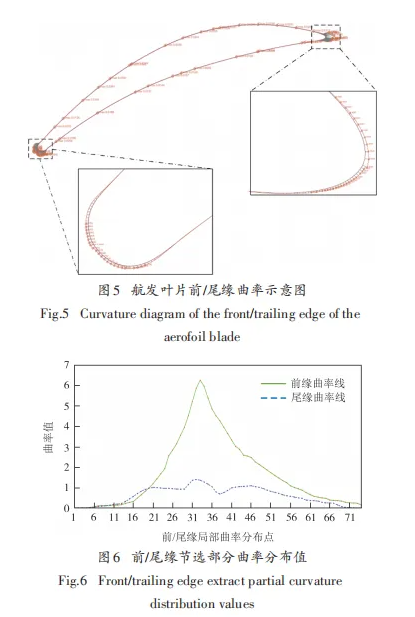
       半赫茲接觸是由Ayasse等［15］在赫茲接觸的基礎上提出的運用于曲率變化大時的求解方法，即在曲率變化小的方向仍然引用赫茲接觸理論，而在接區域曲率變化大的方向上不再采用赫茲接觸理論，其基于接觸輪與葉片前緣的虛擬穿透來對接觸區域進行快速確定. Ma等［16］假設車輪和鋼軌不發生彈性變形，采用半赫茲接觸的虛擬穿透法測定了輪軌接觸區域的接觸斑塊并建立了對應的輪軌接觸模型 .半赫茲接觸可以有效地解決某些赫茲接觸不適用的情況，如圖 5 和圖 6 所示，接觸輪與葉片前緣廓形接觸時，其曲率不斷發生變化，因此使用半赫茲接觸理論對于解決本文研究的砂帶磨削葉片前緣問題具有充足的合理性.

       接觸輪加工葉片前緣時，半赫茲接觸示意圖如圖 7 所示，在接觸區域內沿著葉片曲率變化方向將其劃分為 n 個條帶，帶寬為 Δx，擁有最大高度 H0的條帶稱為母帶，對應的長、短軸曲率分別為 A0、B0，半軸長a和b分別為：

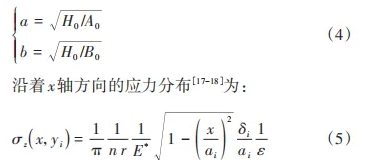
       式中：n為橢圓半軸系數；r為彈性趨近量；E*為等效彈性模量；ai為每一個條帶處的曲率所對應的長半軸；δi為每一個條帶處的曲率所對應的干涉深度；ε為修正系數（針對x軸方向曲率不變）.

       通過 Abaqus 有限元仿真中接觸區域的應力分布，結合課題組自行開發的 CAM 軟件離散待加工葉片的前緣部分，提取加工路徑點 u、v向的曲率 . 根據前緣的曲面特征，沿著葉片邊緣方向（u向）的曲率可近似看作不變，提取曲率變化大的方向（v向）的曲率值，代入式       （4）和式（5）即可求得葉片前緣的應力分布值，進而通過邊緣處應力分布求解該區域的材料去除深度.

       2駐留時間預規劃

       2.1 搭建葉片前緣全局材料去除矩陣

       在第 1 節中，建立了一個葉片前緣部分的材料去除模型，該模型采用修正的 Preston 方程并結合Abaqus有限元仿真 . 本節將針對葉片前緣曲率變化大和難加工的特點，通過軌跡規劃的方法來實現對前緣廓形的加工.首先對于曲面復雜的前緣廓形，通過對比藍光掃描的待加工葉片前緣點云模型和理論數模獲取葉片前緣的加工余量 . 為了解決砂帶柔性磨削接觸面積大和刀位點之間干涉嚴重的問題，本文提出在葉片待加工表面上引入控制點和駐留點，每個控制點對應著待加工表面上相應點的余量，而駐留點則是機器人砂帶磨削時走刀的點位，通過遍歷駐留點和控制點的方式，以精準去除控制點對應余量為目標進行基于駐留時間的軌跡規劃 . 這一軌跡規劃過程可以用對應的矩陣形式表示：

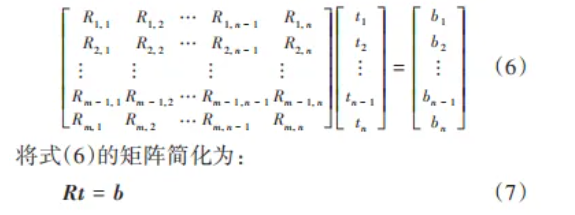
       式中：R為去除函數矩陣，Rm，n表示的是接觸輪在第n個駐留點時對第m個控制點的去除量；t為駐留時間矩陣；b為殘余誤差矩陣.

       航空發動機葉片加工的要求是將待加工葉片與理論廓形之間的殘余誤差 E 控制在公差范圍內 . 利用駐留時間去除葉片邊緣余量的原理是將待加工葉片與理論廓形之間的殘余誤差 E 作為目標函數，去除函數的第n行R（n，：）表示葉片邊緣所有駐留點對第n個控制點的去除能力 . 將 R（n，：）與對應的 tn相乘，可以得到葉片所有駐留點對第 n 個控制點的去除總量. 相對于常規加工方法，這種方法的優勢在于它不僅考慮了接觸點處的材料去除，還考慮了對磨削范圍內其他控制點的去除能力. 此外，通過調整駐留點的疏密程度，合實際工程應用 可以控制加工表面的精度，使其更加符合實際工程應用.

       獲取去除函數矩陣 R 前，由于葉片邊緣曲率變化大，并不像平面一樣可以直接判斷控制點是否位于駐留點的接觸范圍之內，需要對此作出適當的處理. 加工路徑上的接觸判斷圖如圖8所示.本文以任一駐留點為原點，求出當前駐留點的切平面和法矢，以指向下一個駐留點的方向為x軸，法矢和x方向的叉乘作為y軸，建立一個新的局部坐標系.在新的坐標系下以x、y軸作為投影平面將所有控制點投影到該平面上，再通過式（8）的坐標變換矩陣G得到所有控制點在局部坐標系下的坐標.

       式中：（xc，yc，zc）表示駐留點在世界坐標系下的三坐標；（xx，yx，zx）、（xy，yy，zy）和（xz，yz，zz）分別表示局部坐標系下的 X、Y、Z 坐標軸在實際坐標系下的三坐標形式.率法矢夾角小于 控制點在局部坐標系 X 方向的坐標（篩選主曲90°的坐標）如圖9所示.

       本文引入篩選矩陣Q，它由法矢篩選矩陣QA和橢圓接觸篩選矩陣QB組成.由于葉片前緣的曲率變化很大，如果僅按照投影到局部坐標系下的坐標進行橢圓接觸判定，會導致一些控制點無法被正確判定為接觸到.

       因此，根據實際加工情況設置了一個判定控制點和駐留點之間法矢夾角的條件；然后，通過橢圓接觸篩選矩陣 QB進行二次篩選，并將篩選后的投影坐標代入先前求得的材料去除模型中，得到一行的去除函數矩陣. 通過對每一個駐留點進行遍歷，最終可以得到去除函數矩陣R.

       2.2 駐留時間的求解

       R（m，n）矩陣的每一列表示的是路徑上砂帶在每一個駐留點時對該控制點的單位時間材料去除率. 為了保證加工精度，控制點的數量一般是遠遠大于駐留點的數量，并且由于接觸輪的接觸區域相對于工件較小，去除函數矩陣 R 是一個大型的稀疏矩陣. 由于該稀疏矩陣往往是個病態矩陣，向量行數m遠大于列數 n，因此無法獲取精確解，眾多學者從奇異值分解、最小二乘正交分解法（Least Squares QR-Factorization Method，LSQR）、二次規劃尋優等多種角度進行研究和優化，在實際應用中，加工前緣并非需要精確解，大多數情況下，   LSQR 和 Tikhonov 正則化下的解即可滿足加工要求.

       大型稀疏矩陣往往是病態矩陣，LSQR算法并不是直接求出最優解 x，而是遵守最小二乘原則，在限定的空間中尋找最優解. 主要為求解式（9）的線性方程組，且保證其二階殘差范數最小. 

       Tikhonov 正則化則是從提高解的穩定性和減少駐留總時間的角度出發，對去除函數矩陣 R 進行正則化處理，以優化駐留時間 t. 在去除函數矩陣 R 中引入一個數量陣T，數量陣T引入的阻尼因子w表示駐留點密度與表面誤差間的權重關系，理論上 w 的取值區間為［0，+∞），但w的值越小，取得非負駐留時間的可能性越小；而當w的值越大時，加工后的表面誤差也就越大. 矩陣如式（10）所示

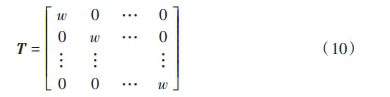
       數量陣 T 將去除函數矩陣 R 由 m 行 n 列擴展為（m+n）行n列的矩陣RW，同時將加工余量列向量b補充 0 以 擴 充 成（m+n）維，基 于 式（6）和 改 進 后 的式（11），將最小二乘問題轉換成虧秩矩陣的求解問題.

       合理地選擇阻尼因子 w 的值，以保證葉片前緣廓形高精度的同時，符合實際加工特點是 Tikhonov正則化的關鍵所在. 去除函數矩陣R如圖10所示.

       2.3 仿真驗證

       為了確定基于駐留時間加工葉片前緣的可能性和尋找合適的阻尼因子w，本文以最終型面誤差E和駐留總時間 Tsum為優化方向設計了 Tikhonov 正則化的仿真試驗 . 葉片前緣駐留點和控制點示意圖如圖11所示.

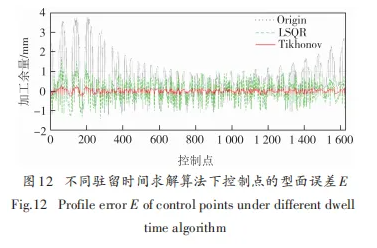
       由圖 11 可知，在葉片前緣處提取 300 個駐留點（紅色點集）和 1 600 個控制點（綠色點集）作為本次仿真試驗的對象 . 本文通過反復迭代調整 Tikhonov正則化中阻尼因子 w 的值，最終選定 w 取 0.4 時最佳 . 圖 12對比了未加工的葉片前緣（Origin）在 LSQR算法和Tikhonov正則化下的最終型面誤差E.由圖12可以明顯看出，2種算法下葉片前緣的加工余量都有所減小，相比較而言，LSQR 算法的去除率在全控制點下約為64.6%，Tikhonov正則化的去除率在全控制點下約為93.6%，因此采用Tikhonov正則化算法下葉片前緣處的型面誤差 E 有著顯著減小，并且葉型趨近于理論廓形.

       3實驗驗證

       第2節通過 MATLAB 的仿真試驗證明了優化葉片前緣廓形的可行性，本節通過實驗驗證基于駐留時間的前緣軌跡規劃在砂帶磨削加工中的有效性.

       本實驗采用的是如圖 13 所示的團隊自行搭建的機器人砂帶磨削平臺，該系統主要由工業機器人、橡膠接觸輪、砂帶、力傳感器和ACF恒力浮動裝置組成 . 采用 Fanuc 工業機器人（M-710IC/50）作為運動載體夾持葉片，磨削力由磨具端的 ACF 恒力浮動打磨裝置（精度 0.1 N）控制，磨削實驗使用 3M 公司生產的粒度為A6（P2000）的237AA金字塔堆積磨料砂帶，線速度為 10 m/s，法向磨削力為 5 N. 根據駐留時間 ti，j和兩個駐留點間的步長 hi-1j和 hi，j可以計算出Fanuc機器人的進給速度vi，j，如式（12）所示.

       圖 14（a）為未加工的葉片實物圖，圖 14（b）為基于駐留時間調控的對前緣5%~95%葉高處進行磨削加工后的葉片.

        通過對比磨削前、后的葉片前緣廓形，可以明顯看出磨削后的葉片邊緣更加光順，表面粗糙度也有了顯著降低. 采用GOM三維藍光掃描儀對磨削后葉片進行檢測，將采集到的點云模型與理論模型進行比對. 圖15為磨削后前緣不同截面輪廓線和尺寸偏差，分別提取了葉高的30%、50%和70%葉片處截面廓形，截面包含了理論廓形（光滑彩色線條）與其加工的公差帶（棕色區域），不規則曲線段為前緣的實際加工廓形，兩曲線間的差值表示實際加工廓形與理論廓形之間的差距 . 由圖 15 可以看出，葉片前緣廓形誤差相較于未加工之前有了明顯的減小，前緣廓形線基本處于+0.03~-0.05 mm 的公差帶之間，與理論廓形之間的型面誤差E在0.02 mm以內.

       4結論

       本文針對壓氣機葉片前緣柔性磨削接觸狀態不明，廓形精度難控制的問題，制的砂帶磨削方法 提出了基于駐留時間控，具體的研究結論如下：

       1）考慮葉片邊緣狹窄區域內曲率急變的特征，將半赫茲接觸理論引入柔性磨具和葉片邊緣的接觸問題求解，初步求解了接觸區域內的應力分布，通過Abaqus有限元仿真對接觸部分的應力分布曲線進行了驗證和修正，基于獲取的應力分布和 Preston 方程建立了葉片前緣的材料去除模型.

       2）基于材料去除模型，遍歷控制點搭建了全局材料去除模型矩陣，建立了駐留時間求解線性方程組. 以加工余量最小化作為目標函數，引入帶有阻尼因子的 Tikhonov 正則化，求解駐留時間分布并轉化為進給速度，仿真表明余量有效去除達到93.6%.

       3）在課題組自行搭建的機器人砂帶磨削平臺上開展了葉片前緣磨削實驗，結果表明，磨削后的葉片前緣輪廓線基本在+0.03~-0.05 mm 的公差帶之間，與理論模型之間的型面誤差E在0.02 mm以內，證明了本文所提方法能夠實現葉片前緣的精準加工.