引言
麻花鉆頭生產的兩個主要磨削步驟為排屑槽磨削和后刀面磨削,其磨削參數決定了鉆頭的幾何參數。像頂角和鉆芯厚度等就是鉆頭制造參數的隱函數。
在排屑槽磨削中,砂輪原地旋轉,同時鉆頭繞軸旋轉并向下移動。鉆頭的這種雙重運動控制著排屑槽的螺旋角和位置,而砂輪的斷面形狀則控制著排屑槽的橫剖面。上述磨削步驟以正交位置進行兩次就生產出雙排屑槽鉆頭。在后刀面磨削中,砂輪繞著固定軸旋轉形成一個圓錐半角θ的磨錐(圖1所示),鉆頭繞著磨錐軸旋轉。以上磨削步驟以對稱位置進行兩次就生產出雙后刀面。這些側面可以看成是磨錐的截面。
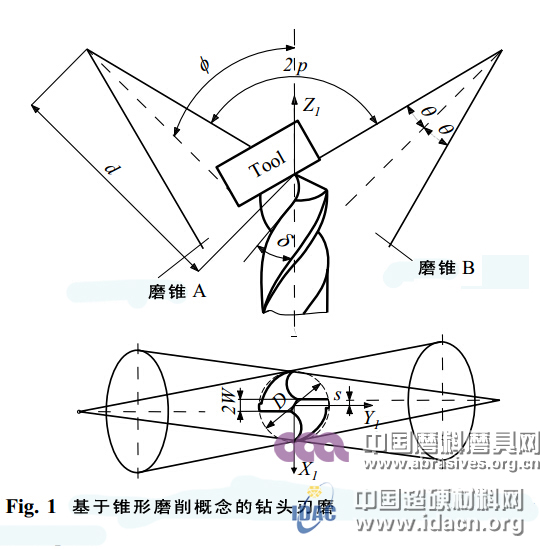
本研究利用計算機輔助設計(CAD)對鉆槽生產中的砂輪設計進行研究。利用MATLAB工具進行CAD建模,并得出實驗結果和討論。
實驗方法
1. 建立坐標系和設置變量
為了對排屑槽設計輪廓、鉆頭螺旋溝槽面和砂輪斷面形狀進行建模,建立如圖2所示的坐標系。
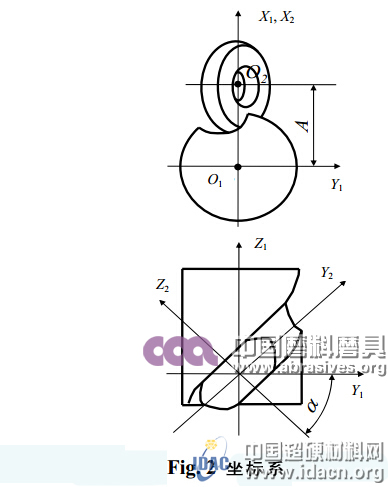
鉆頭螺旋溝槽坐標O1—X1Y1Z1設置為移動坐標,砂輪坐標O2—X2Y2Z2設置為固定坐標。
研磨機有三個設置變量:Y1上砂輪裝置角α,Z2上砂輪偏置WO,螺旋溝槽和砂輪的垂直軸間距A≈W+Rg (Rg是砂輪最大直徑)。
2. 排屑槽設計輪廓建模
鉆頭橫截面要設計得當側面被研磨時能夠出平行切削刃。鉆頭排屑槽輪廓分為6部分,如圖3所示。
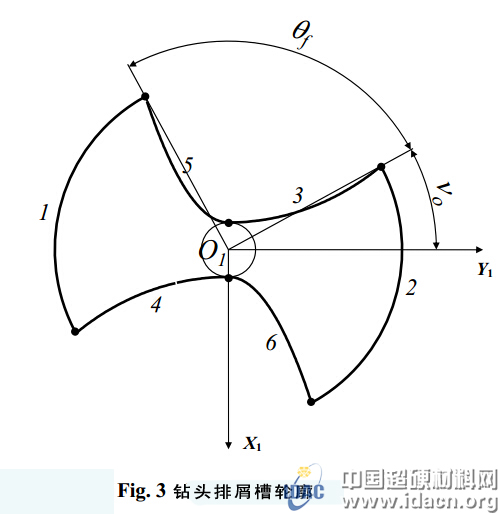
當鉆槽型面設計用連續曲線表示時,鉆頭排屑槽型面的主切削刃部分由理輪廓線可得,后刀面部分用拋物線表示。由此可以得出鉆頭輪廓斜面的顯式表達式。為求得平行切削,主切削刃型面用連續曲線表示如下:
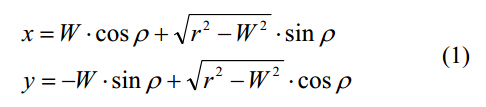
其中,r是從鉆芯厚度W的一半到鉆頭半徑R的變量:
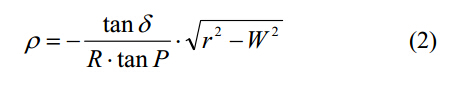
主切削刃表達式如下:
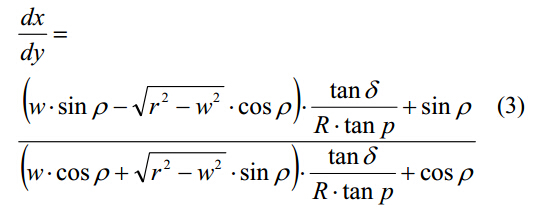
根據切削刃排屑槽的理論型面,橫刃前角表達式如下:
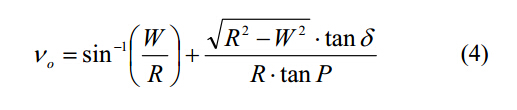
因此,排屑槽輪廓的在預設坐標系中的定向就可以固定下來。
后刀面輪廓可以用拋物線表示,表達式如下:
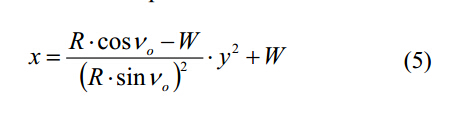
鉆頭型面的后刀面斜面表達式如下:
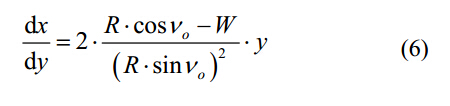
3. 螺旋排屑槽表面公式
沿著鉆頭軸向給排屑槽添加一個螺旋運動,就可以對螺旋排屑槽表面進行建模:
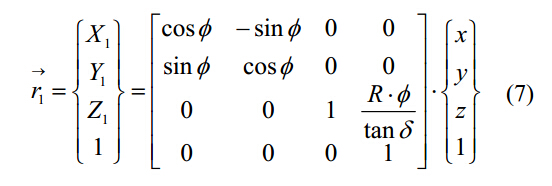
其中:Φ是鉆頭螺旋輪廓繞Z1軸的輔助變量,順著Z1軸方向觀察,Φ是順時針方向的。公式7在鉆頭軸O1—X1Y1Z1轉化為O2—X2Y2Z2時可表達為:
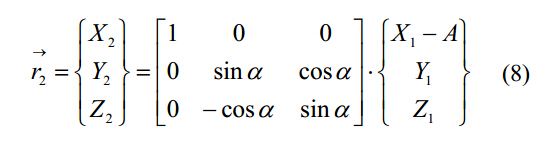
4. 螺旋排屑槽表面和砂輪間的相切曲線
螺旋排屑槽表面和砂輪間的相切曲線可以用矢量公式表達如下:
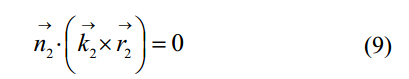
其中,K2={0 0 1}T是Z2軸的單位向量;n2是螺旋排屑槽表面和砂輪在O2—X2Y2Z2坐標的每一個切點的法向量,表達如下:
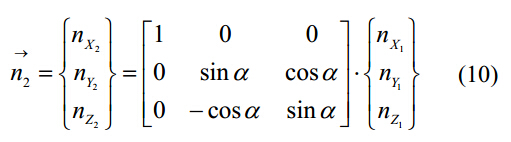
其中,n1是螺旋排屑槽表面和砂輪在O1—X1Y1Z1坐標的每一個切點的法向量,表達式如下:
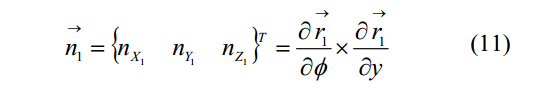
其中:
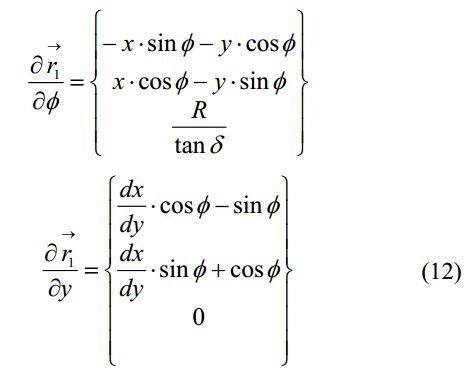
將式(8)和(10)替換為式(9),相切曲線公式就表達為以下解析式:
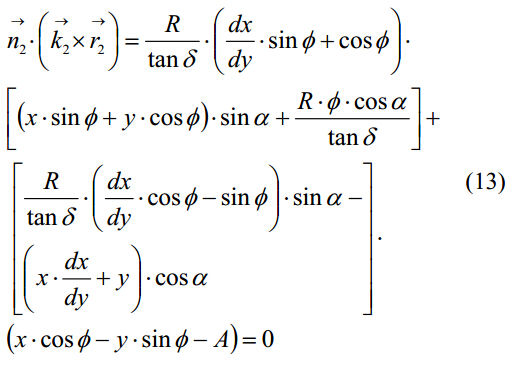
5. 砂輪輪廓計算
在求得相切曲線后,將相切曲線繞著砂輪軸旋轉即得到砂輪表面;平面上的砂輪輪廓表達式如下:
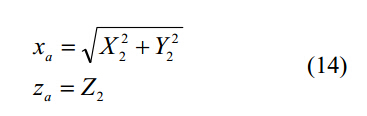
對于本實驗中的自動鉆槽研磨機,求得的離散砂輪輪廓通過兩條圓弧實現曲線擬合。
6.砂輪偏置計算
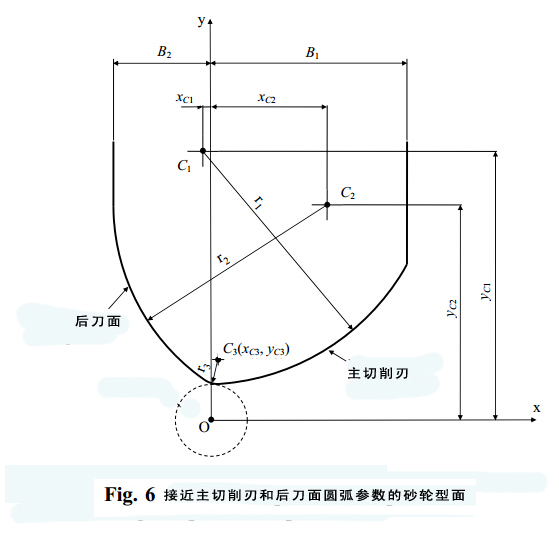
砂輪偏置WO可以通過圖4顯示的理論砂輪型面求得。
圖4
理論主切削刃和后刀面在非連續性M上交叉。很顯然這樣的輪廓型面不太實際可行,不能造出對應的排屑槽設計型面。相反,曲線AMB顯示的且在M處有非連續性的砂輪型面就能夠滿足該條件。此處應注意的是,非連續性M點處的砂輪直徑也是砂輪的最大直徑Dg。此外,沿著砂輪軸的非連續的位置代表了砂輪偏置WO。
實驗結果
本研究利用MATLAB工具建立了砂輪設計CAD模型。圖形用戶界面(GUI)如圖5所示:
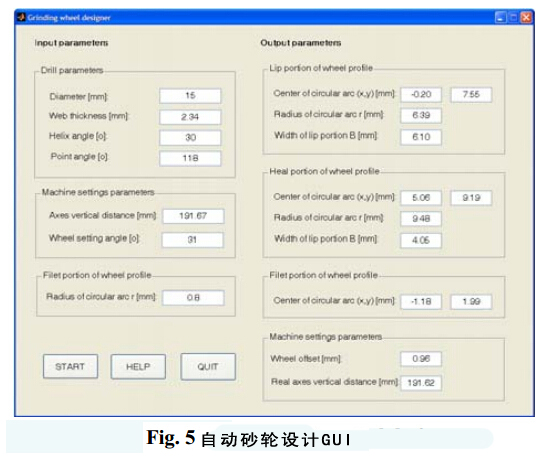
在砂輪型面設計過程中,用到了鉆頭直徑、螺旋角、頂角、鉆芯厚度、砂輪裝置角、GUI垂直距離等輸入參數。GUI還包括輸出參量,如中心坐標、圓弧半徑以及圖6所顯示的砂輪偏置。
為求得以下輸入參數,圖7展示了一個砂輪輪廓:
D= 15 mm, 2p= 118°, ?= 30°, 2W= 2.34 mm, A =191.67 mm,α= (30 ÷ 35)°.
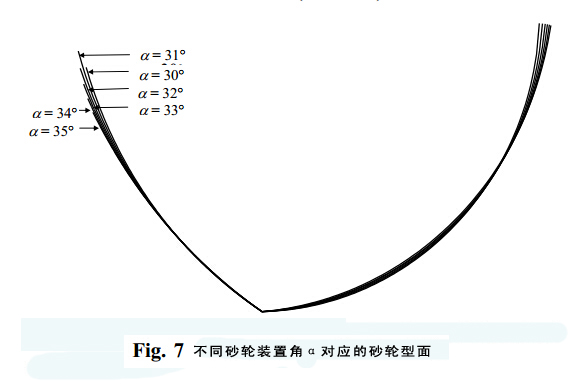
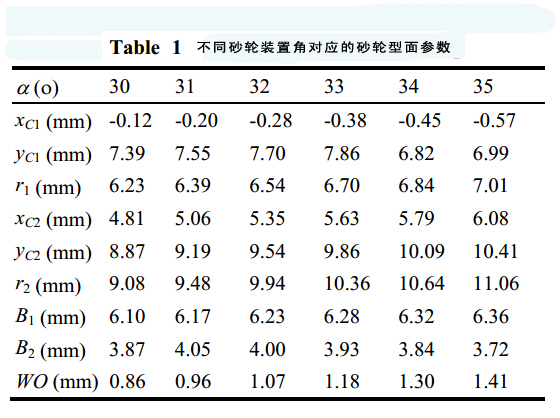
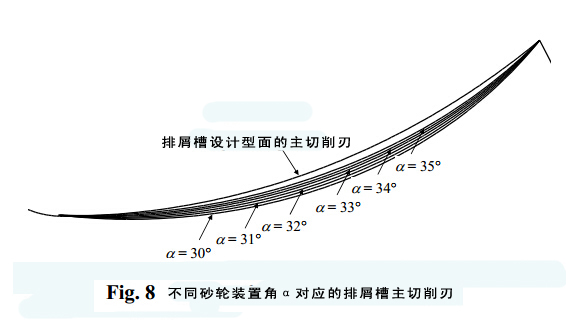
表1是不同砂輪裝置角對應的砂輪輪廓參數值。圖8是不同砂輪裝置角對應的主切削刃。
結論
本研究中的自動砂輪設計程序簡化了麻花鉆排屑槽生產工藝設計,縮短了選擇最佳砂輪幾何形狀的時間。該CAD模型還可以用來修改其他機器設置變量從而獲得排屑槽型面設計的最接近值。


 手機資訊
手機資訊 官方微信
官方微信







 豫公網安備41019702003604號
豫公網安備41019702003604號